江端智一さんが公開されている、「お金に愛されないエンジニア」のための新行動論(4)でDockerで株価データのデータベースを作って、Golangのシミュレーションプログラムを実行しpythonでグラフを描いてみるまでを真似してみた。
eetimes.itmedia.co.jp
江端さんのGitHubをcloneするとDドライブ直下にmoneyフォルダができる。

money1フォルダまでおりて(docker-compose.ymlファイルがあるフォルダ)
> docker-compose up -d
とするとバックグラウンドでDockerが起動している(doker-compose startは不要)
>docker-compose ps

>docker exec -it postgres bash
ここからWindows10環境からDocker上のlinux環境に遷移
#psql -U postgres
ここからPostgreSQL環境に遷移
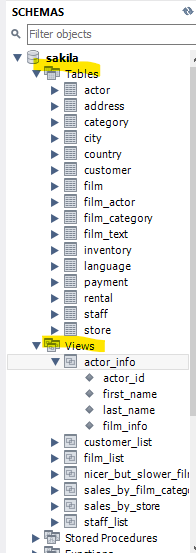
hitachi,toushiba,jfe,sharpのデータベースを作る。それぞれのデータベースにstockというテーブルを作っていくが一部変数定義をintではなくrealに変更する。ここではhitachiを例にする
hitachi=#CREATE TABLE stock(Date varchar(10),Open int,High int,Low int,Close int,Ave5day real,Ave25day real,Ave75day real,VWAP real,Vol int,Vol5day int,Vol25day int);
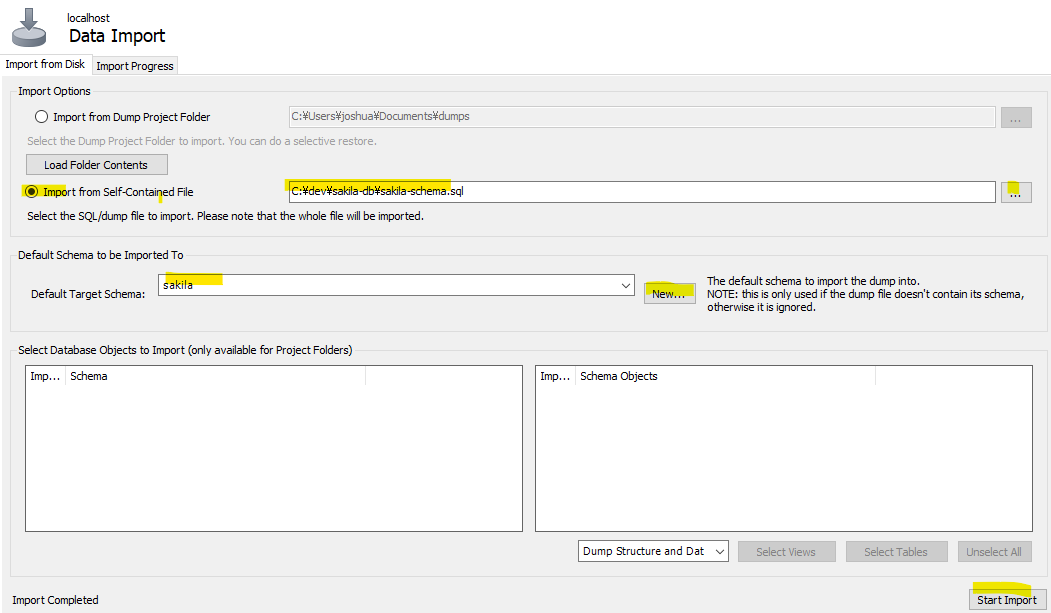
テーブルができたので、ここにcsvファイルからimportしていく。
終了したらPostgreSQL環境からDocker環境に戻る。
d:money/money1で別のWindows環境を起動する。ホルダ内にmain.goがあることを確認しておく。
シミュレーションプログラムを実行。このプログラムは一つのデータベースに対して実行されるのでhitachiデータベースのシミュレーションがしたい場合はプログラムの一部を書き換えて計4回実行し結果をcsvファイルの書き込む。
>go run main.go > hitachi.cvs
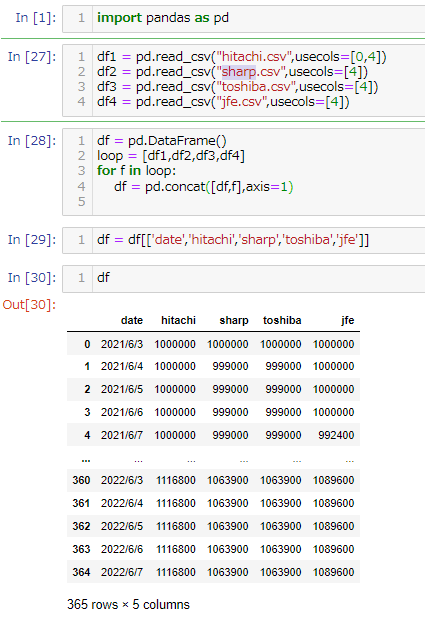
csvファイルのヘッダを「date,close,stock_value,cash,hitachi」にする。何故か文字コードがutf16LEになっているのでutf-8に強制的に変更した。

Window10からjupyter notebookを起動していろいろグラフを書いてみる。最後のグラフが4つ要素があるのにグラフが3つしかないようにみえるのはtoshiba.csvのデータとSharp.csvファイルのデータが同一なので上書きされて3つにしか見えないように見える。